Primeiro vamos definir o que são sequências numéricas:
São sequência de números, finitas ou infinitas, na forma (a1, a2, a3, …, an) que obedecem a uma lei de formação.
Veja o exemplo abaixo.
Sequência = {2; 3; 4; 5; 6…}
Percebemos que cada termo tem uma unidade a mais que o anterior.
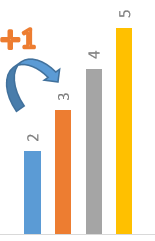
Progressão Aritmética
É um tipo de sequência numérica em que a diferença entre diferença entre quaisquer dois números consecutivos é sempre constante. Essa diferença é chamada de razão da PA.
De maneira mais geral:
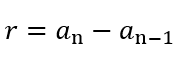
Podemos fazer a mesma análise no seguinte gráfico.
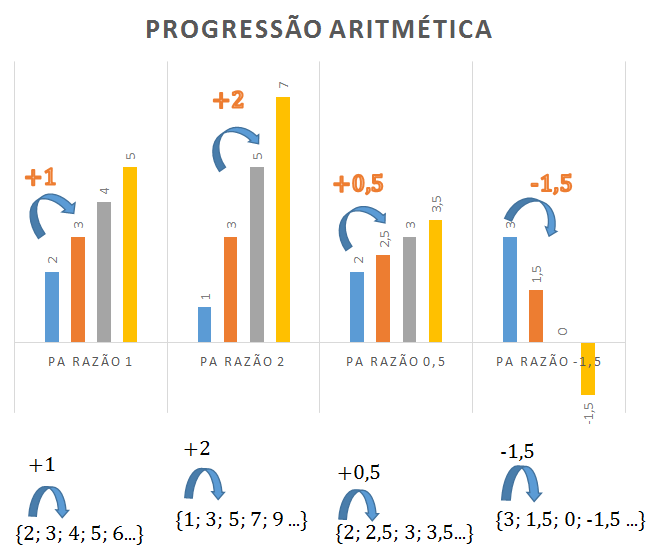
Podemos estabelecer a lei geral da PA através da soma das equações abaixo:
Também podemos encontrar o termo n em função do termo k:
Agora vejamos como fazer a soma da PA.
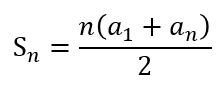
Veja agora a seguinte questão de concurso público:
FCC – TJ TRF2/TRF 2/Administrativa/”Sem Especialidade”/2012
Considere que os termos da sucessão seguinte foram obtidos segundo determinado padrão.
(20, 21, 19, 22, 18, 23, 17, …)
Se, de acordo com o padrão estabelecido, X e Y são o décimo e o décimo terceiro termos dessa sucessão, então a razão Y/X é igual a:
a) 44%.
b) 48%.
c) 56%.
d) 58%.
e) 64%.
Vamos resolver essa questão de duas maneiras, a maneira que todo mundo resolve e a maneira fácil.
Primeiro, a maneira que todo mundo resolve. Percebemos o seguinte padrão entre os números da sequência:
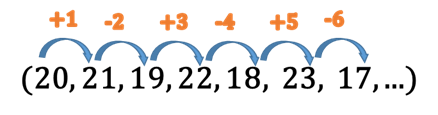
Seguindo esta linha de raciocínio, conseguimos encontrar o 10° e o 13° termos.
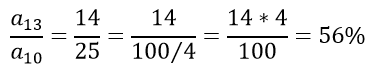
Mas sinceramente, na prova o tempo é escasso!
Então, é muito mais útil perceber que temos duas PAs na mesma sequência, veja as cores diferentes:
Assim, basta ir completando as sequências até achar o termo 10° e o 13°:
Dividindo o 13° termo pelo 10° conforme a questão pede, temos:
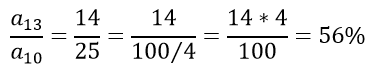
Parabéns, você resolveu em menos de 60 segundos e gabaritou.
Letra C.
Inscreva-se na nossa newsletter e receba mini simulados e resumos pra você gabaritar sua prova.
Susane Ribeiro. Eng. Aeronáutica do ITA. Turma 2009.
