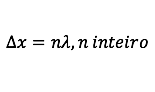O trombone de Quincke é um dispositivo experimental utilizado para demonstrar o fenômeno da Interferência de ondas sonoras. Uma fonte emite ondas sonoras de determinada frequência na entrada do dispositivo. Essas ondas se dividem pelos dois caminhos (ADC e AEC) e se encontram no ponto C, a saída do dispositivo, onde se posiciona um detector. O trajeto ADC pode ser aumentado pelo deslocamento dessa parte do dispositivo. Com o trajeto ADC igual ao AEC, capta-se um som muito intenso na saída. Entretanto, aumentando-se gradativamente o trajeto ADC, até que ele fique como mostrado na figura, a intensidade do som na saída fica praticamente nula. Desta forma, conhecida a velocidade do som no interior do tubo (320 m/s), é possível determinar o valor da frequência do som produzido pela fonte.
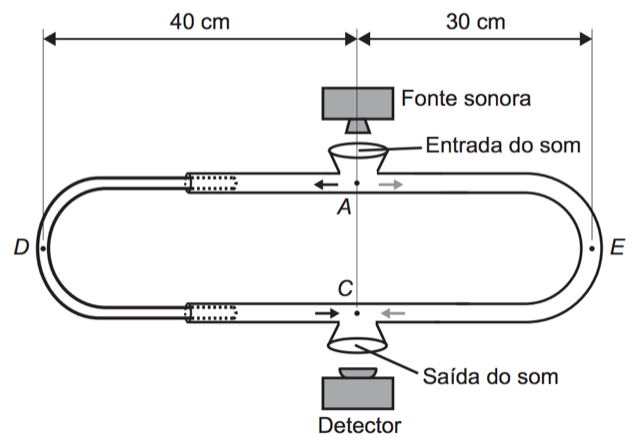
O valor da frequência, em hertz, do som produzido pela fonte sonora é
- 3200
- 1600
- 800
- 640
- 400.
Solução
Para não haver som na saída do trombone, a intensidade deste som deve ser nula, um fenômeno que cancela a intensidade do som é a interferência destrutiva entre ondas sonoras.
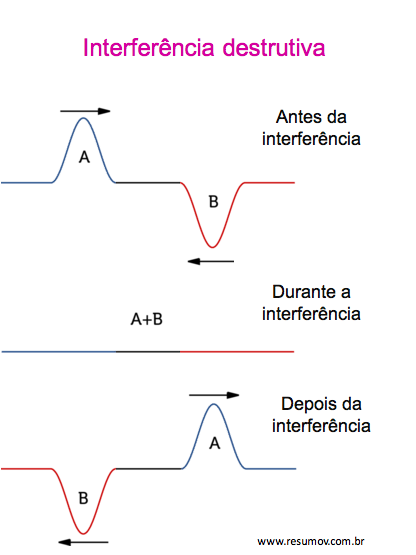
A interferência destrutiva é consequência da defasagem entre as duas ondas, que é causada pela diferença entre as distâncias percorridas por cada uma. A partir da figura, podemos ver que a diferença Δx entre os caminhos percorridos por cada onda é de 20 cm.
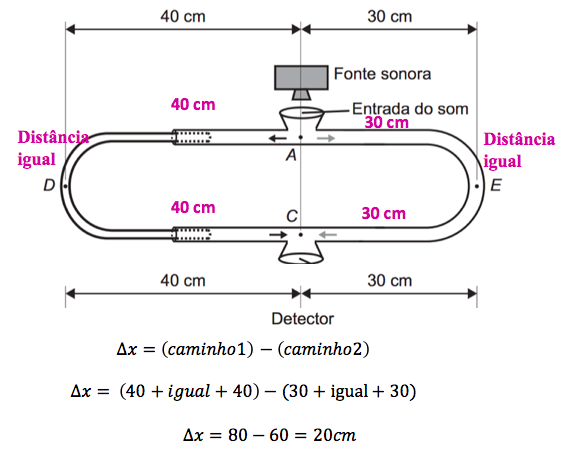
Na interferência destrutiva temos a seguinte equação:
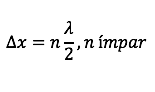
com n=1:
![]()
Agora resta usarmos a equação fundamental da ondulatória, lembrando que a questão forneceu a velocidade do som.
Uma dica para lembrar da equação abaixo é a frase: “Vai lamber ferida“ (V=lambda*frequência)
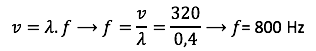
Letra C
Veja como é a interferência construtiva, que aumenta a intensidade da onda final.
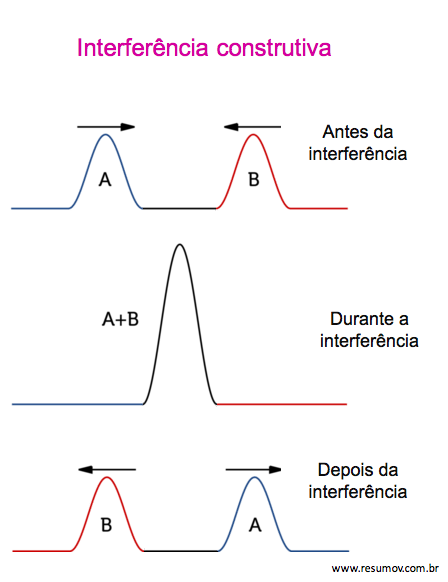
No caso da interferência construtiva a equação seria: